C. Gauer+, A. Wixforth+, J.P. Kotthaus+, M. Kubisa#,W. Zawadzki▀, B. Brar*, and H. Kroemer*
+Sektion Physik der LMU München, D-80539 München, Germany
#Institute of Physics, Polish Academy of Sciences, 02-668 Warsaw,
Poland
▀Institute for Experimental Physics, Univ. of Innsbruck, A-6020
Innsbruck, Austria
permanent adress: Institute of Physics, Polish Academy of Sciences, 02-668
Warsaw, Poland
*Department of Electrical and Computer Engineering, UC Santa Barbara, CA 93106,
USA
Abstract. Resonances between hybrid magneto-electric subbands in InAs/AlSb quantum wells have been studied in the Voigt configuration. The simultaneous observation of both spin-conserving and spin-flip transitions allows us to determine experimentally the influence of the depolarization effect on the resonance energy and the lineshape. We demonstrate that the spin-conserving transitions are driven by the in-plane magnetic field and that the relevant optical matrix elements can be deduced from the magnetic field dependence of the oscillator strength. The spin-flip resonances, on the other hand, are made possible by the bulk inversion-asymmetry of InAs.
1. Introduction
The collective and single-particle excitations of a two-dimensional electron gas in semiconductor heterostructures have been the subject of sustained investigations both experimentally and theoretically during the last two decades. Narrow-gap semiconductors offer interesting possibilities because the strong interband coupling results in pronounced band nonparabolicity and strong spin-orbit interaction leading to large spin g-values. Also, the effects of inversion asymmetry, as present in zinc-blende materials [1], are particularly pronounced in narrow-gap systems. It was found that this inversion asymmetry can lead to a zero-field spin-splitting [2] and to an enhanced probability for the excitation of spin-flip resonances [3].
Here, we report on the investigations of optical transitions between hybrid magneto-electric subbands (HMES) on InAs/AlSb multi-quantum wells. The HMES are formed when the magnetic field has a component transverse to the direction of the electric confinement. It is well known that intersubband transitions (IST) are usually allowed only for the light polarization parallel to the direction of electric confinement. We demonstrate that an in-plane magnetic field breaks this polarization selection rule and makes possible the observation of intersubband transitions for the polarization perpendicular to the magnetic field. Moreover, the optical matrix element can be determined by measuring the magnetic field dependence of the oscillator strength. The bulk inversion asymmetry of InAs allows the excitation of combined intersubband spin-flip transitions. The energetic difference between both resonances directly gives the depolarization shift. We also demonstrate that the depolarization strongly reduces the line-broadening caused by the non-parallel dispersion of the subbands in narrow-gap materials.
2. Experiment
The multi-quantum well described here was grown on a GaAs substrate followed by a 1um AlSb buffer and a 10 period superlattice [4] to accomodate the strain between the substrate and the active layers. The 20 period multi-quantum well consisting of 15 nm InAs layers and Te-d -doped AlSb barriers of 10 nm width had a topmost barrier of 55nm width in order to minimize band-bending effects induced by the surface charge [5]. The carrier density per well is 2.5.1012cm-2 at T = 4.2K as determined by the classical Hall effect.
Mid infrared (MIR) spectra were taken using a rapid scan Fourier transform spectrometer with the sample mounted in Voigt-geometry. Experimentally, we determined the relative change in MIR transmission T(B!=0)/T(B=0) of the unpolarized radiation for different in-plane magnetic fields B. We also measured transmission spectra under oblique incidence ratioing against a reference substrate. All experiments were performed at low temperatures T = 4.2K with a Cu-doped germanium photoconductor as a detector.

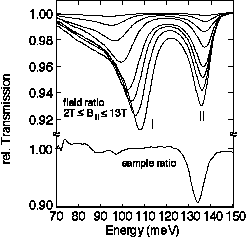
Fig. 1: The upper traces show transmission spectra of our InAs/AlSb multi-quantum well in the magnetic field ratio at in-plane magnetic fields B=2T, 4T, 6T, 8T, 10T, 11T, 12T, and 13T. The lower trace is a spectrum of the same sample ratioed against a reference substrate with the radiation incident under an oblique angle.
In Fig. 1a we show the experimental data for magnetic fields between B=2T and B=13T measured in the Voigt geometry (inset of Fig. 2). The reference spectrum is the one taken at zero magnetic field. We observe two resonances: one at around E=100meV (I) and a second at E=135meV (II). As confirmed by ratioing against a reference substrate there is no resonant absorption in the quantum well at B=0T. We therefore conclude that both resonances are induced by the in-plane magnetic field and strongly gain oscillator strength at high fields. The position of line I shifts to higher energies with increasing magnetic field, whereas the position of line II remains almost constant. Line II is also much narrower and more symmetric than line I.
Fig. 1b shows a spectrum of the same sample taken at an oblique angle of 57[[ring]] ratioed against a reference substrate. The resonance observed at E=135meV is identified as an IST from both its polarization dependence and theoretical calculations. Therefore we interpret resonance II in Fig. 1a also as an IST as the energetic position and lineshape are almost identical in both cases. However, no resonance corresponding to line I of Fig. 1a is observed in Fig. 1b at zero magnetic field.
3. Interpretation
Spin-conserving IST are usually shifted to energies above the single particle energy differences by depolarization effects whereas spin-flip excitations are not affected by the depolarization field as revealed by inelastic light scattering experiments [7]. Calculating the depolarization shift for our system we find that it roughly corresponds to the energetic difference between lines I and II for B->0T. As the oscillator strength of both resonances I and II depends on the magnetic field in a very similar manner we conclude that line II is a combined spin-flip intersubband resonance. This interpretation is further corroborated by the linewidth of the resonances. As shown in [8] the non-parabolicity induced line-broadening is greatly reduced by the depolarization field. This is exactly what we find experimentally: Line I (interpreted as the spin-flip transition) is much broader than the spin-conserving resonance II at all fields.
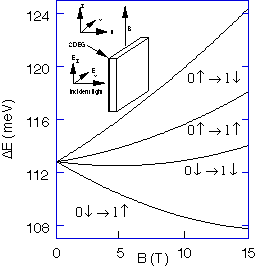
Fig. 2: Single particle transition energies between the HMES. The inset shows schematically our experimental geometry.
First, we explain the possibility of exciting an IST in the Voigt geometry by
in-plane polarized light. Choosing the electric confinement to be in the
y-direction and the magnetic field in the z-direction the electronic
wavefunction for the n-th subband can be written as
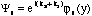 [6]. From this general form of the wavefunction it can be seen that the
interaction Hamiltonian must be a function of y in order for the intersubband
matrix element to be non-zero. With the gauge
[6]. From this general form of the wavefunction it can be seen that the
interaction Hamiltonian must be a function of y in order for the intersubband
matrix element to be non-zero. With the gauge
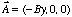 the interaction Hamiltonian for light polarized in the x-direction [[alpha]]x
is found to be
the interaction Hamiltonian for light polarized in the x-direction [[alpha]]x
is found to be
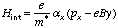 .
Here, the last term is y-dependent for B!=0, resulting in a matrix element
proportional to the magnetic field
.
Here, the last term is y-dependent for B!=0, resulting in a matrix element
proportional to the magnetic field
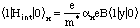 (1)
(1)
For the polarization parallel to the magnetic field [[alpha]]z the IST matrix
element still remains zero at finite fields. It follows from the above
reasoning that the intensity I of the IST should vary as I
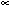 B2
which is what we observe experimentally for line II. This magnetic field
dependence provides an alternative way to measure the optical matrix elements
of the IST as shown in [9] for GaAs quantum wells. In the case of InAs,
however, a quantitative analysis requires that the narrow band gap situation
and in particular the energy dependent electronic mass be taken into account.
B2
which is what we observe experimentally for line II. This magnetic field
dependence provides an alternative way to measure the optical matrix elements
of the IST as shown in [9] for GaAs quantum wells. In the case of InAs,
however, a quantitative analysis requires that the narrow band gap situation
and in particular the energy dependent electronic mass be taken into account.
To this end we calculate the electron energies for a potential well U(y) in
the presence of an external magnetic field
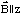 .
The band-strucure of InAs is accounted for within the three-level
.
The band-strucure of InAs is accounted for within the three-level
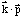 model as described in [10]. From this calculation we find that all subbands are
spin-split at finite magnetic fields. Therefore four transitions become
possible between the two lowest electrical subbands: Two are spin-conserving
and two involve a spin-flip. In Fig. 2 we plot the magnetic field dispersion
for these transitions for k||=0. In this calculation the screening effects have
been taken into account by fist order perturbation theory. It is seen that the
energy of the two spin-conserving excitations has only a very weak magnetic
field dependence while the spin-flip transitions are more widely separated at
high fields. At high values of k|| (kF=4x106cm-1 in our
sample) all resonance energies are strongly reduced (about 35meV at k||=kF) as
a result of the non-parallel subband dispersions. Furthermore, the magnetic
field dependence also decreases drastically at high k||. This explains why we
are not able to resolve all four transitions in our experiment: The
nonparabolicity-induced broadening is much larger than the energetic separation
of the spin-flip resonances which results in one broad line. The
spin-conserving transitions, however, show only very weak magnetic field
dependence and are subject to the depolarization shift, hence resulting also in
a single symmetric and narrow resonance.
model as described in [10]. From this calculation we find that all subbands are
spin-split at finite magnetic fields. Therefore four transitions become
possible between the two lowest electrical subbands: Two are spin-conserving
and two involve a spin-flip. In Fig. 2 we plot the magnetic field dispersion
for these transitions for k||=0. In this calculation the screening effects have
been taken into account by fist order perturbation theory. It is seen that the
energy of the two spin-conserving excitations has only a very weak magnetic
field dependence while the spin-flip transitions are more widely separated at
high fields. At high values of k|| (kF=4x106cm-1 in our
sample) all resonance energies are strongly reduced (about 35meV at k||=kF) as
a result of the non-parallel subband dispersions. Furthermore, the magnetic
field dependence also decreases drastically at high k||. This explains why we
are not able to resolve all four transitions in our experiment: The
nonparabolicity-induced broadening is much larger than the energetic separation
of the spin-flip resonances which results in one broad line. The
spin-conserving transitions, however, show only very weak magnetic field
dependence and are subject to the depolarization shift, hence resulting also in
a single symmetric and narrow resonance.
We now determine the oscillator strength of the spin-conserving and spin-flip
transitions by calculating the matrix elements for the electric dipole
excitations with the interaction Hamiltonian in the matrix form
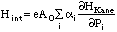 .
Here, A0 is the amplitude of the vector potential, Pi the canonical momentum
with i
.
Here, A0 is the amplitude of the vector potential, Pi the canonical momentum
with i
 (x,y,z)
and HKane corresponds to the 8-band matrix Hamiltonian. The multi-band
calculation yields for the matrix element
(x,y,z)
and HKane corresponds to the 8-band matrix Hamiltonian. The multi-band
calculation yields for the matrix element
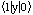 =31.0Å.
Measuring the absorption under an oblique angle as shown in Fig. 1 we obtain a
somewhat lower value of 24.5Å from the experiment. Evaluating (1) for the
magnetic field induced IST
=31.0Å.
Measuring the absorption under an oblique angle as shown in Fig. 1 we obtain a
somewhat lower value of 24.5Å from the experiment. Evaluating (1) for the
magnetic field induced IST
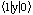 is found to be 25.0Å thus giving almost the same value as in the
conventional absorption measurement. This very good agreement proves that in
the Voigt configuration an accurate determination of the matrix elements is
indeed possible.
is found to be 25.0Å thus giving almost the same value as in the
conventional absorption measurement. This very good agreement proves that in
the Voigt configuration an accurate determination of the matrix elements is
indeed possible.
The question remains as to why the excitation of spin-flip transitions is so
remarkably effective in our experiment. It is well known that strong interband
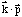 -coupling
and spin-orbit interaction result in a possibility of spin-flip transitions in
narrow-gap materials. However, this mechanism is too weak to account for the
strong spin-flip resonances as observed experimentally. On the other hand, it
was shown theoretically by Rashba and Sheka [3] and later confirmed
experimentally by Chen et al. [11] that the inversion asymmetry of the crystal
also gives rise to spin-flip excitations. This mechanism should predominate at
large
-coupling
and spin-orbit interaction result in a possibility of spin-flip transitions in
narrow-gap materials. However, this mechanism is too weak to account for the
strong spin-flip resonances as observed experimentally. On the other hand, it
was shown theoretically by Rashba and Sheka [3] and later confirmed
experimentally by Chen et al. [11] that the inversion asymmetry of the crystal
also gives rise to spin-flip excitations. This mechanism should predominate at
large
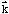 -values
as present in our sample.
-values
as present in our sample.
In our 8x8
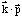 matrix the dominant inversion asymmetry terms have the schematic form
G(PiPj+PjPi), where G is a material constant. These terms give only small
corrections to the electron energies, but they strongly enhance the possibility
of spin-flip transitions at large
matrix the dominant inversion asymmetry terms have the schematic form
G(PiPj+PjPi), where G is a material constant. These terms give only small
corrections to the electron energies, but they strongly enhance the possibility
of spin-flip transitions at large
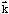 -values.
Since the strength of the inversion asymmetry terms is not yet known for InAs
we take a value similar to that of InSb
-values.
Since the strength of the inversion asymmetry terms is not yet known for InAs
we take a value similar to that of InSb
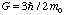 [12]. We quantitatively describe the depolarization effects in our system by
generalizing the approach of Ando [13] for mixed spins. In the computation we
assume a level broadening
[12]. We quantitatively describe the depolarization effects in our system by
generalizing the approach of Ando [13] for mixed spins. In the computation we
assume a level broadening
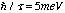 .
While the detailed results of the theory are given in [14] we would like to
present here the general features: The inversion asymmetry gives rise to
spin-flip IST excited by the same light polarization [[alpha]]x that also
causes the spin-conserving transitions. Both types of excitations - spin-flip
and spin-conserving - have roughly the same strength. Although we deal with
four transitions, our calculations predict only two peaks in agreement with the
experiment. Both the oscillator strength and the position of the resonances
agree quantitatively with the experimental data.
.
While the detailed results of the theory are given in [14] we would like to
present here the general features: The inversion asymmetry gives rise to
spin-flip IST excited by the same light polarization [[alpha]]x that also
causes the spin-conserving transitions. Both types of excitations - spin-flip
and spin-conserving - have roughly the same strength. Although we deal with
four transitions, our calculations predict only two peaks in agreement with the
experiment. Both the oscillator strength and the position of the resonances
agree quantitatively with the experimental data.
We my add that in a recent experiment carried out in a strip-line geometry we also found spectroscopic evidence for a zero-field spin-splitting in the sample described here. The magnitude of the splitting is roughly 10meV which is in reasonable agreement with the predictions made in [2].
4. Conclusion
To summarize, we have observed both spin-flip and spin-conserving intersubband optical transitions in InAs/AlSb quantum wells subjected to an in-plane magnetic field. The external field makes possible the observation of spin-conserving resonances although the incident light is polarized in the plane of the two-dimensional electron gas. This mechanism also allows us to measure the matrix elements relevant for IST. The spin-flip intersubband excitations are induced by the bulk inversion asymmetry of InAs. Our results demonstrate that the depolarization field drastically reduces the linewidth of the spin-conserving transitions while the depolarization shift can be deduced from the energetic difference between the spin-flip and spin-conserving resonances.
The work in Munich was sponsored by the Volkswagen Stiftung. The Santa Barbara group gratefully acknowledges support from the Office of Naval Research and from QUEST, the NSF Science and Technology Center for Quantized Electronic Structures (Grant DMR 91-20007).
References
[1] Kane E O 1957 J. Phys. Chem. Solids 1 249
[2] Lommer G, Malcher F and Rössler U Phys. Rev. Lett. 60, 728 (1992)
[3] Rashba E I and Sheka V I 1961 Fiz. Tverd. Tela 3 1735; ibid. 3 1863 (1961 Sov. Phys. Solid State 3 1257)
[4] Tuttle G, Kroemer H and English J H 1989 J. Appl. Phys. 65 5239
[5] Nguyen C, Brar B, Kroemer H and English J H 1992 Appl. Phys. Lett. 60 1854
[6] Zawadzki W 1987 Semicond. Sci. Technol. 2 550
[7] Pinczuk A and Abstreiter G 1989 in Light Scattering in Solids V, edited by M. Cardona and G. Güntherodt (Berlin: Springer Verlag) p 153
[8] Zaluzny M 1991 Phys. Rev. B 43 4511
[9] Gauer C, Wixforth A, Kotthaus J P, Abstreiter G, Weimann G and Schlapp W, submitted for publication
[10] Zawadzki W, Klahn S and Merkt U 1986 Phys. Rev. B 33 6916
[11] Chen Y F, Dobrowolska M, Furdyna J K and Rodriguez S 1985 Phys. Rev. B 32 890
[12] Kane E O 1980, in Narrow Gap Semiconductors. Physics and Applications, edited by W. Zawadzki (Berlin: Springer Verlag) p 13
[13] Ando T 1978, J. Phys. Soc. Jpn. 44 475
[14] Gauer C, Wixforth A, Kotthaus J P, Kubisa M, Zawadzki W, Brar B and Kromer H, submitted for publication